Method Combinations
Configuration class: ConfigUnion
While different efficient fine-tuning methods and configurations have often been proposed as standalone, combining them for joint training might be beneficial.
To make this process easier, adapters provides the possibility to group multiple configuration instances using the ConfigUnion class.
For example, this could be used to define different reduction factors for the adapter modules placed after the multi-head attention and the feed-forward blocks:
from adapters import BnConfig, ConfigUnion
config = ConfigUnion(
BnConfig(mh_adapter=True, output_adapter=False, reduction_factor=16, non_linearity="relu"),
BnConfig(mh_adapter=False, output_adapter=True, reduction_factor=2, non_linearity="relu"),
)
model.add_adapter("union_adapter", config=config)
Mix-and-Match Adapters
Configuration class: MAMConfig
He et al. (2021) study various variants and combinations of efficient fine-tuning methods.
They propose Mix-and-Match Adapters as a combination of Prefix Tuning and parallel bottleneck adapters.
This configuration is supported by adapters out-of-the-box:
from adapters import MAMConfig
config = MAMConfig()
model.add_adapter("mam_adapter", config=config)
and is identical to using the following ConfigUnion:
from adapters import ConfigUnion, ParBnConfig, PrefixTuningConfig
config = ConfigUnion(
PrefixTuningConfig(bottleneck_size=800),
ParBnConfig(),
)
model.add_adapter("mam_adapter", config=config)
Papers:
Towards a Unified View of Parameter-Efficient Transfer Learning (He et al., 2021)
UniPELT
Configuration class: UniPELTConfig
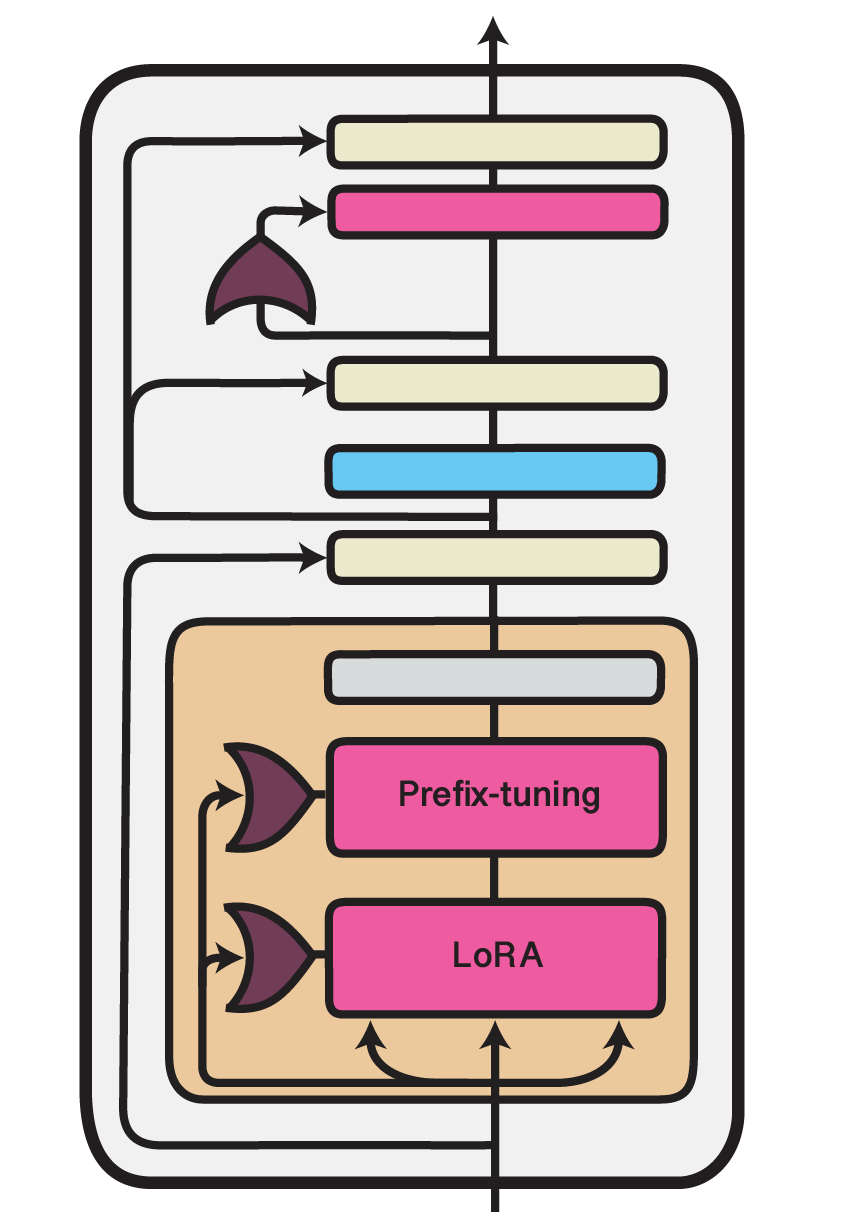
Illustration of the UniPELT method within one Transformer layer. Trained components are colored in shades of magenta.
An approach similar to the work of He et al. (2021) is taken by Mao et al. (2022) in their UniPELT framework. They, too, combine multiple efficient fine-tuning methods, namely LoRA, Prefix Tuning and bottleneck adapters, in a single unified setup. UniPELT additionally introduces a gating mechanism that controls the activation of the different submodules.
Concretely, for each adapted module \(m\), UniPELT adds a trainable gating value \(\mathcal{G}_m \in (0, 1)\) that is computed via a feed-forward network (\(W_{\mathcal{G}_m}\)) and sigmoid activation (\(\sigma\)) from the Transformer layer input states (\(x\)):
These gating values are then used to scale the output activations of the injected adapter modules, e.g., for a LoRA layer:
In the configuration classes of adapters, these gating mechanisms can be activated via use_gating=True.
The full UniPELT setup can be instantiated using UniPELTConfig1:
from adapters import UniPELTConfig
config = UniPELTConfig()
model.add_adapter("unipelt", config=config)
which is identical to the following ConfigUnion:
from adapters import ConfigUnion, LoRAConfig, PrefixTuningConfig, SeqBnConfig
config = ConfigUnion(
LoRAConfig(r=8, alpha=2, use_gating=True),
PrefixTuningConfig(prefix_length=10, use_gating=True),
SeqBnConfig(reduction_factor=16, use_gating=True),
)
model.add_adapter("unipelt", config=config)
Finally, as the gating values for each adapter module might provide interesting insights for analysis, adapters comes with an integrated mechanism of returning all gating values computed during a model forward pass via the output_adapter_gating_scores parameter:
outputs = model(**inputs, output_adapter_gating_scores=True)
gating_scores = outputs.adapter_gating_scores
Note that this parameter is only available to base model classes and AdapterModel classes.
In the example, gating_scores holds a dictionary of the following form:
{
'<adapter_name>': {
<layer_id>: {
'<module_location>': np.array([...]),
...
},
...
},
...
}
Papers:
UNIPELT: A Unified Framework for Parameter-Efficient Language Model Tuning (Mao et al., 2022)